Primary Neon, Magnesium, and Silicon Fluxes

Primary cosmic rays Ne, Mg, and Si are thought to be mainly produced and accelerated in astrophysical sources. Precise knowledge of their spectra in the GV - TV rigidity range provides important information on the origin, acceleration, and  propagation processes of cosmic rays in the Galaxy. The precision measurement of the primary cosmic rays He, C, and O fluxes has revealed an identical rigidity dependence of these three fluxes above 60 GV, including the  unexpected deviation from a single power law (hardening) of their spectra above $\sim$200 GV. Precision study of differences in the rigidity dependence of Ne, Mg, and Si compared to He, C, and O provide new insights into the origin and propagation of cosmic rays [M.J. Boschini et al., Astrophys. J. 840, 115 (2017); M.J. Boschini et al., Astrophys. J. 858, 61 (2018)] probing the existence of  non-homogeneous diffusion, since heavier cosmic rays propagate shorter distances [G. Jóhannesson et al., Astrophys. J. 824, 16 (2016)].  

There have been no measurements of Ne, Mg, and Si fluxes as functions of rigidity, and over the last 30 years only few measurements exist in kinetic energy per nucleon [J. J. Engelmann et al., Astron. Astrophys. 233, 96 (1990); S. Swordy et al., Astrophys. J. 349, 625 (1990); H. S. Ahn et al., Astrophys. J. 715, 1400 (2010); H. S. Ahn et al., Astrophys. J. 714, L89 (2010); H. S. Ahn et al., Astrophys. J. 707, 593 (2009); K.A. Lave et al., Astrophys. J. 770, 117 (2013); J.A. Esposito et al., Astroparticle Physics 1, 33 (1992); M. Ichimura et al. Phys. Rev. D 48, 1949 (1993); A. D. Panov et al., Bull. Russian Acad. Sci. 73, 564 (2009); F. Gahbauer, G. Hermann, J. R. Hörandel, D. Müller, and A. A. Radu, Astrophys. J. 607, 333 (2004); M. Ave, P. J. Boyle, F. Gahbauer, C. Höppner, J. R. Hörandel, M. Ichimura, D. Müller, and  A. Romero-Wolf, Astrophys. J. 678, 262 (2008)]. Typically these measurements have errors larger than 20% at 50 GeV/n. 

We present the precision measurements of the Ne, Mg, and Si fluxes in the  rigidity range from 2.15 GV to 3.0 TV  basedon 1.8 million Ne, 2.2 million Mg, and 1.6 million Si nuclei. Figure 1 shows the rigidity dependence of the Ne, Mg, and Si fluxes with the total errors, the sum in quadrature of statistical and systematic errors. As seen,  the total error is $\sim$5% at 100 GV for each flux (corresponding to kinetic energy of $\sim$50 GeV/n). 

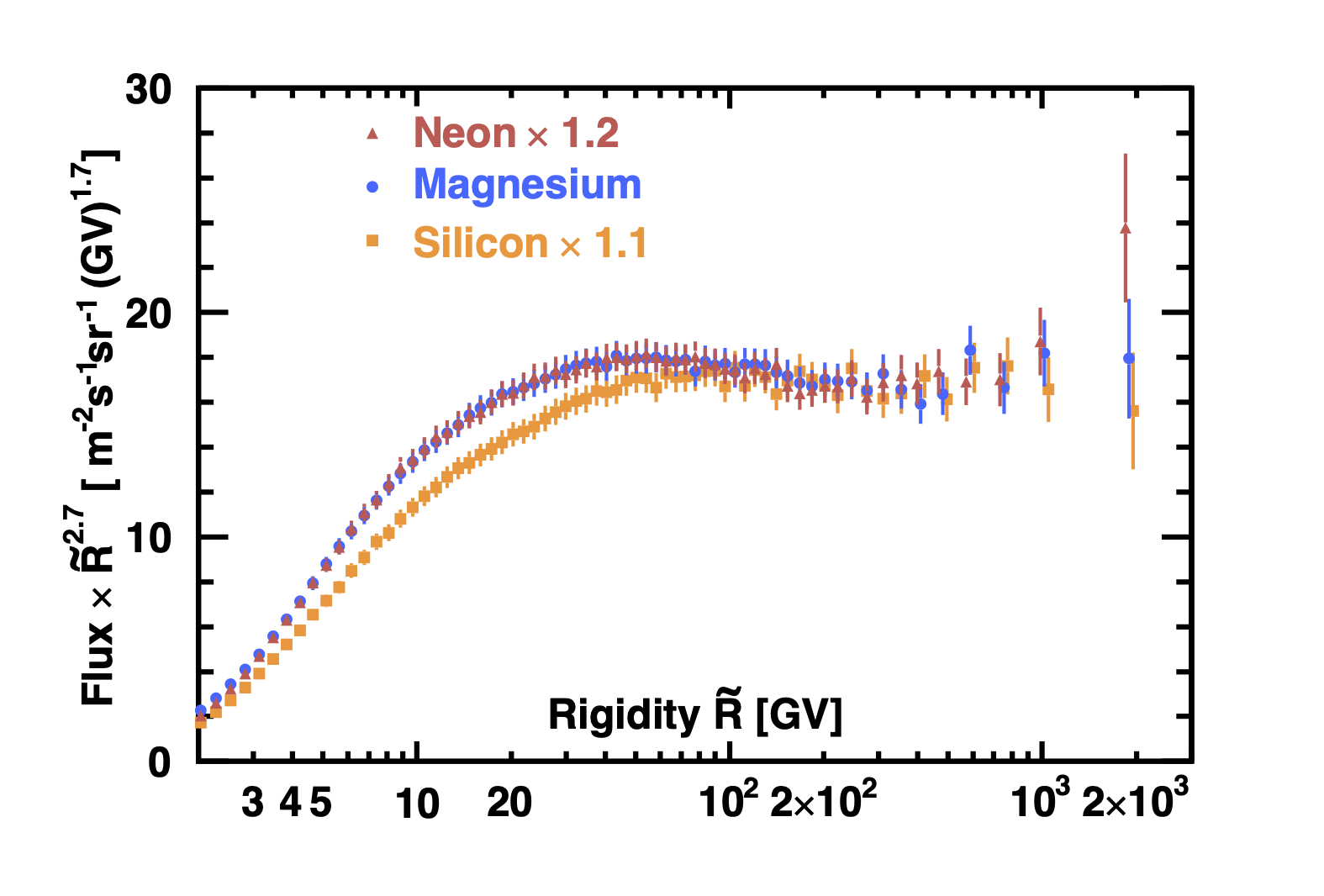
Figure 2a shows the Ne and Mg fluxes and Ne/Mg flux ratio, and Figure 2b the Si and Mg fluxes and Si/Mg flux ratio, as  functions of rigidity $\tilde{R}$.

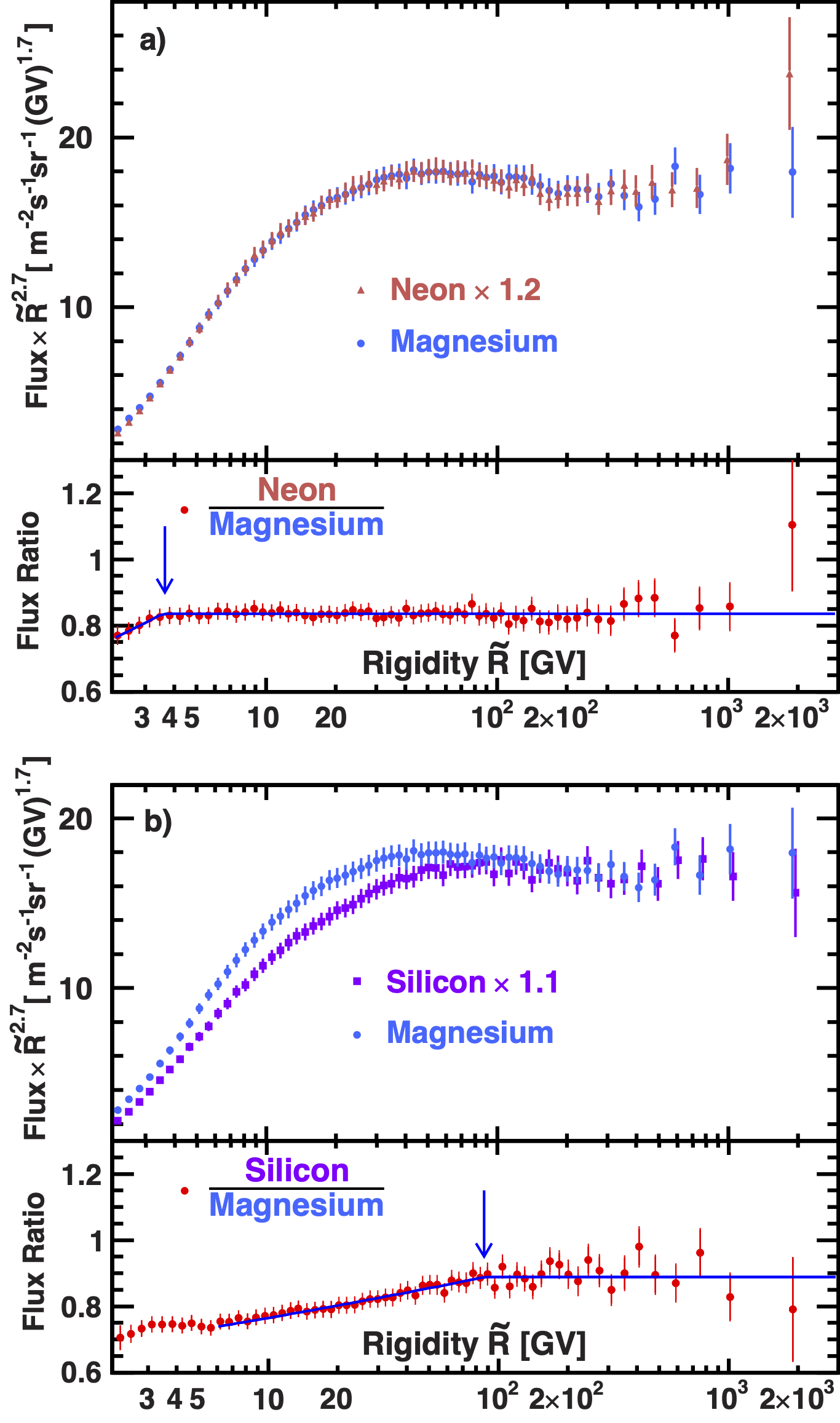
To establish the rigidity intervals where the Ne, Mg, and Si fluxes have identical rigidity dependence, the fits of Ne/Mg and Si/Mg ratios have been performed to 
$$
\frac{\Phi_\mathrm{Ne,Si} }{\Phi_\mathrm{Mg}} =
\begin{cases} 
     k \, (R/R_0)^{\Delta},    & R \le R_{0}, \\
     k \, ,                    & R >   R_{0}.
\end{cases}
\label{eq:dplc2} \tag{1}
$$

For  the Ne/Mg ratio, the fit yields
$$
\begin{align*}
k^{\mathrm{Ne/Mg}}      & = 0.84\pm0.02, \\
R_0^{\mathrm{Ne/Mg}} & = 3.65\pm0.5\,\mathrm{GV}, \\
\Delta^\mathrm{Ne/Mg} & = 0.19\pm0.08, \\
\mathrm{with}\,\, \chi^2/\mathrm{d.o.f.}        & = 42/64 \,\, \mathrm{over\,\, the\,\, entire\,\, rigidity\,\, range}. 
\end{align*}
$$

From the fit results we  found that the Ne and Mg fluxes  have an identical rigidity dependence above 3.65 GV. Note that AMS has also observed an identical rigidity dependence  above 7 GV between secondary cosmic ray Li and B  fluxes.

For  the Si/Mg ratio, the fit yields   
$$
\begin{align*}
k^{\mathrm{Si/Mg}}      & = 0.89\pm0.02, \\
R_0^{\mathrm{Si/Mg}} & = 86.5\pm13\,\mathrm{GV}, \\
\Delta^\mathrm{Si/Mg} & = 0.069\pm0.005, \\
\mathrm{with}\,\, \chi^2/ \mathrm{d.o.f.}        & = 29/53 \,\, \mathrm{above\,\, 6\,GV}.
\end{align*}
$$

From the fits results we conclude that all  three  fluxes have an identical rigidity dependence above 86.5 GV. 
 
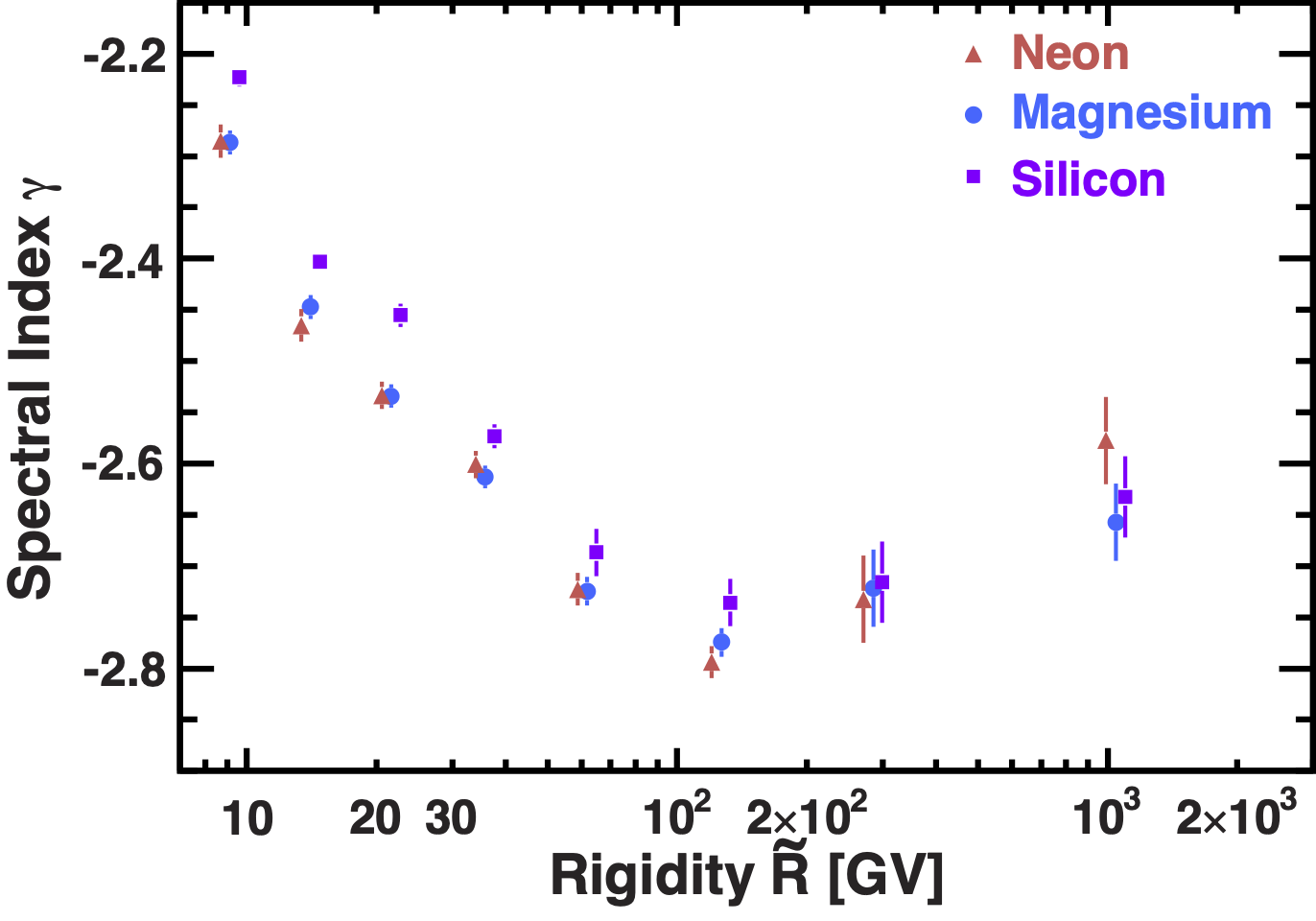
To examine the rigidity dependence of the fluxes, the variation of the flux spectral indices $\gamma$ with rigidity was obtained in a model independent way using $\Delta = d[\log(\Phi_{S}/\Phi_{P})/d[\log(R)]$ over non-overlapping rigidity intervals bounded by 7.09, 12.0, 16.6, 28.8, 45.1, 86.5, 192.0, 441.0 and 3000.0 GV. The results are presented in Figure 3. As seen, the Ne and Mg spectral indices are identical in this rigidity range and the three flux  spectral indices  harden identically with rigidity above $\sim$200 GV.

To compare  the rigidity dependence of the Ne, Mg, and Si fluxes  with that of He, C, and O primary cosmic ray fluxes, which have identical rigidity dependence above 60 GV, the ratios of the neon, magnesium, and silicon  fluxes to the characteristic primary cosmic ray oxygen flux (Table) were fitted to the double power law 
$$ 
\frac{\Phi_\mathrm{Ne,Mg,Si} }{\Phi_\mathrm{O}} =
\begin{cases} 
     C \, (R/86.5\mathrm{GV})^{\Delta},  & R \le 86.5~\mathrm{GV}, \\
     C \,  (R/86.5\mathrm{GV})^{\delta}, & R >   86.5~\mathrm{GV}, 
\end{cases}
\label{doublepl1} \tag{2}
$$
where $C$ is a constant,  to the ratios for  rigidities above 20 GV have been performed and shown in Figure 4.

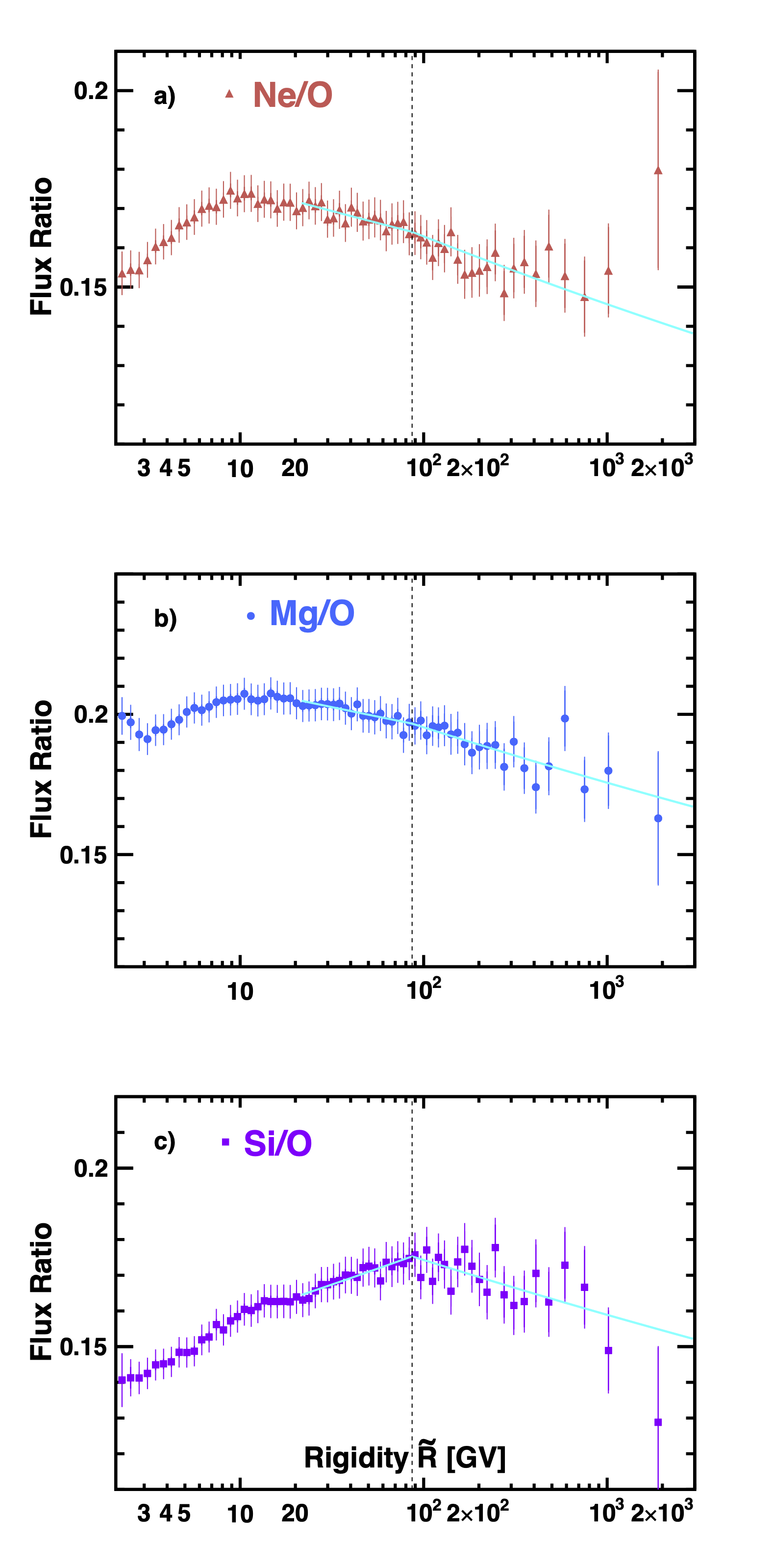
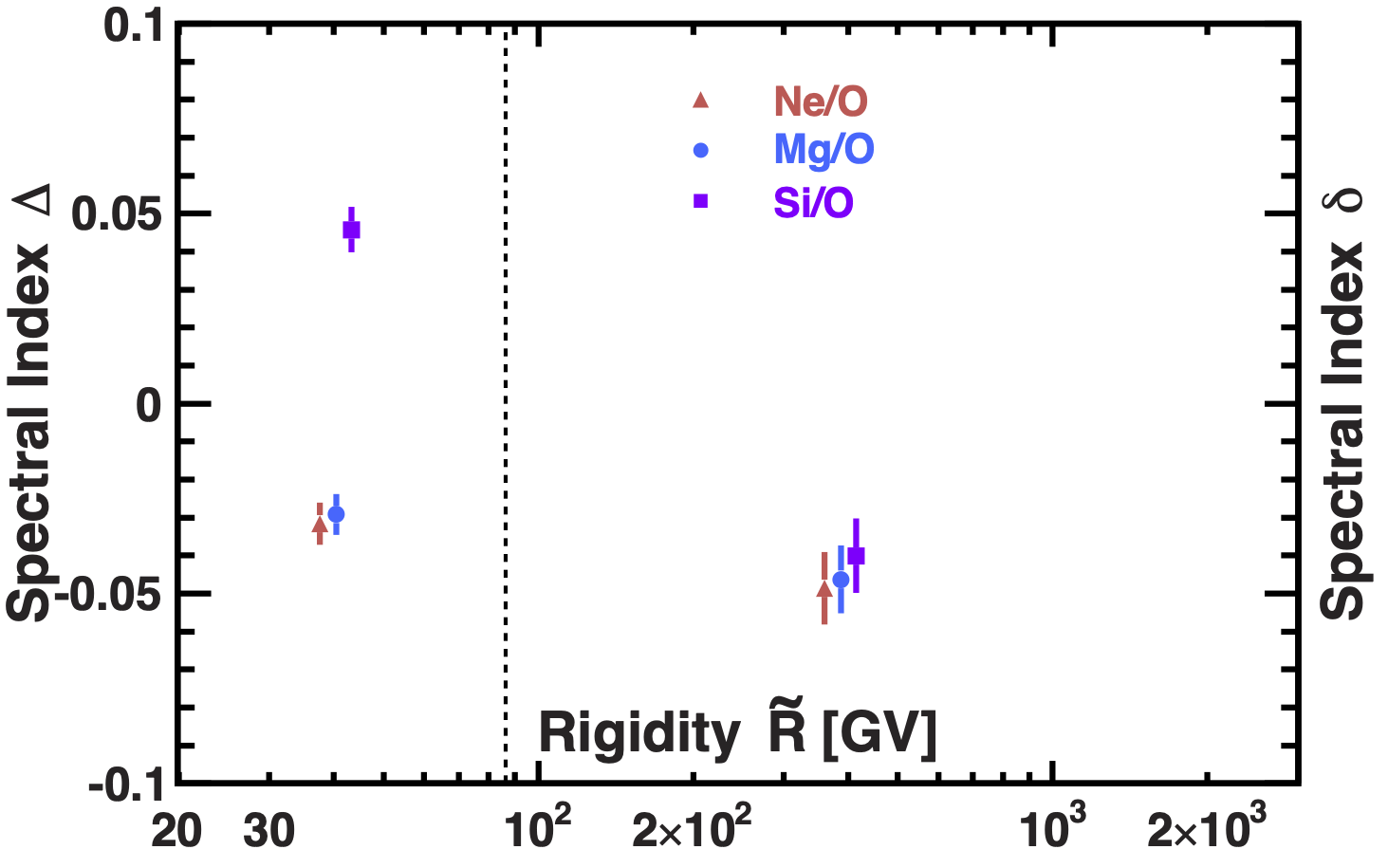
Figure 5 shows the rigidity dependence of the spectral indices  Ne/O, Mg/O, and Si/O obtained from the fits. As seen, above $86.5$ GV the spectral indices are 
$$
\begin{align*}
\delta^\mathrm{Ne/O} & = -0.046 \pm 0.010, \\
\delta^\mathrm{Mg/O} & =-0.049 \pm 0.011, \\
\delta^\mathrm{Si/O}  & = -0.040\pm0.011,
\end{align*}
$$
fully compatible with each other. Their average value  is 
$$
\begin{align*}
\langle\delta\rangle & =-0.045\pm 0.008.
\end{align*}
$$

The difference of $\langle\delta\rangle$ from zero by more than 5$\sigma$ shows  that the Ne, Mg, and Si is a different class of primary cosmic rays than He, C, and O.

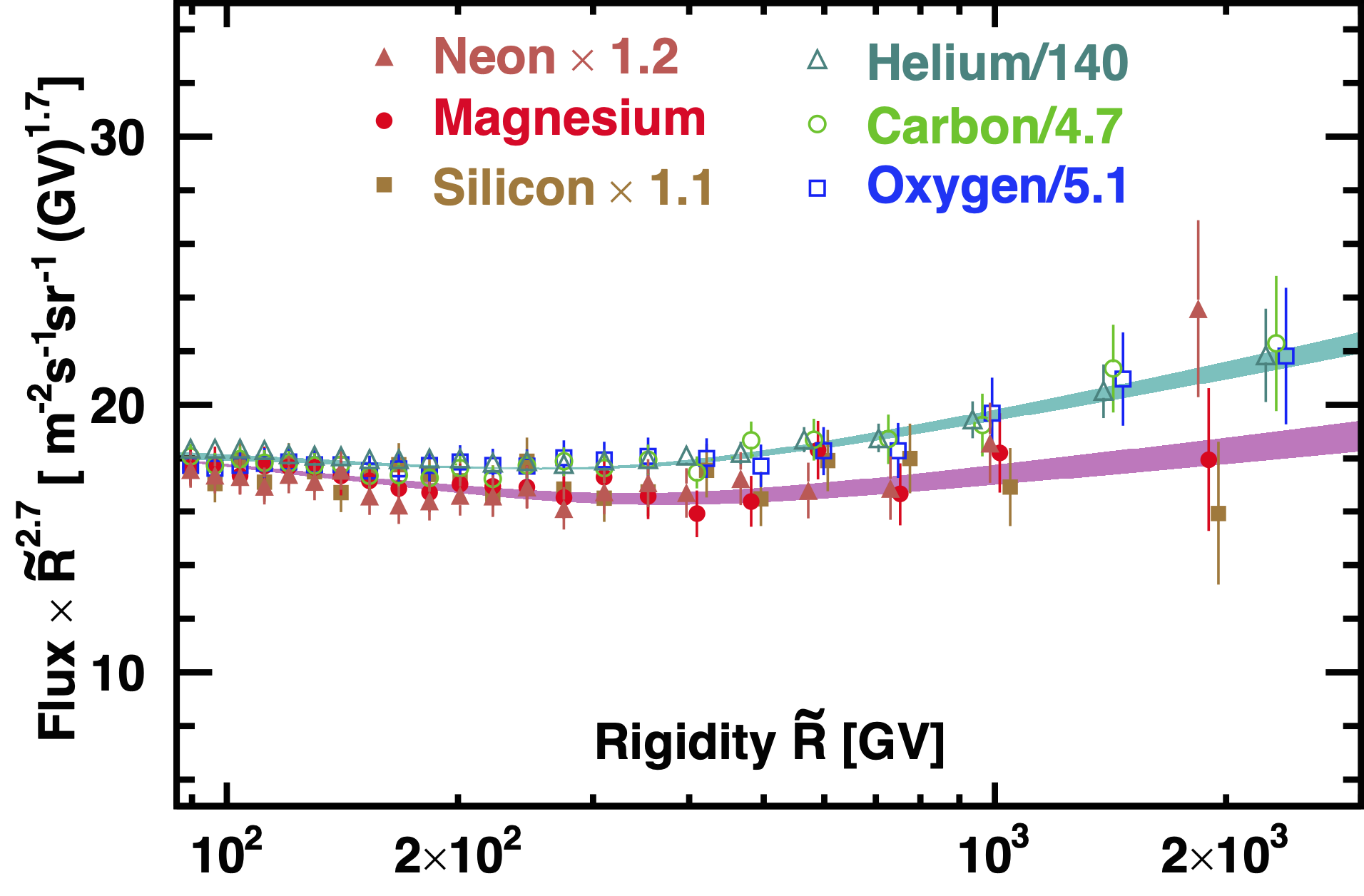
This is illustrated in Figure 6, which shows the rigidity dependence of the  Ne, Mg, and Si fluxes compared to rigidity dependence of the He, C, and O fluxes (Tables SM I-III of Phys. Rev. Lett. 119, 251101). 

$$ \Phi =  C \left(\frac{R}{45\,\mathrm{GV}}\right)^\gamma \left[ 1 +\left(\frac{R}{R_0}\right)^{{\Delta\gamma}/{s}}\right]^s \label{eq:proton_fit} \tag{3}$$ 

Fitting the He, C and O fluxes over the rigidity range 60 GV to 3 TV with Eq. \ref{eq:proton_fit}  simultaneously with common parameters  $s$, $\gamma$, $R_0$,  $\Delta\gamma$ yields 
$$
\begin{align*}
C_\mathrm{He}                & = (950\pm10) \times10^{-4}\,\, \mathrm{m}^{-2} \mathrm{sr}^{-1}  \mathrm{s}^{-1}\, \mathrm{GV}^{-1}, \\
C_\mathrm{C}                  & = (31\pm1) \times10^{-4}\,\, \mathrm{m}^{-2} \mathrm{sr}^{-1}  \mathrm{s}^{-1}\, \mathrm{GV}^{-1}, \\
C_\mathrm{O}                  & = (33\pm1) \times10^{-4}\,\, \mathrm{m}^{-2} \mathrm{sr}^{-1}  \mathrm{s}^{-1}\, \mathrm{GV}^{-1}, \\
\gamma_\mathrm{HeCO} & = -2.756  \pm 0.002, \\
\Delta\gamma                   & = 0.170 \pm 0.015, \\
s                                        & = 0.05 \pm 0.015, \\
R_0                                   & = 340^{+40}_{-30}\, \mathrm{GV}.
\end{align*}
$$

The fit result for He, C, and O fluxes together with the 68% C.L. band are shown in Figure 6.

The fit of the normalization parameters $C_\mathrm{Ne}, C_\mathrm{Mg}$, and $C_\mathrm{Si}$ was  performed  on the Ne, Mg, and Si fluxes together with Eq. \ref{eq:proton_fit} above 86.5 GV  fixing the   $\gamma_\mathrm{NeMgSi}$,  $\Delta\gamma$, $s$, and $R_0$ parameters. We used the $\Delta\gamma$, $s$, and $R_0$  values obtained from the simultaneous fit to the  He, C, and O fluxes and $\gamma_\mathrm{NeMgSi}  = \gamma_\mathrm{HeCO} +\langle\delta\rangle$, where $\langle\delta\rangle=-0.045$ is the average spectral index of Ne/O, Mg/O and Si/O flux ratios above 86.5 GV, see  Eq. \ref{doublepl1}. The fit yields 
$$
%\addtolength{\jot}{1em}
\begin{align*}
C_\mathrm{Ne} & =(5.6\pm0.2) \times10^{-4}\,\, \mathrm{m}^{-2} \mathrm{sr}^{-1}  \mathrm{s}^{-1}\, \mathrm{GV}^{-1}, \\
C_\mathrm{Mg} & =(6.7\pm0.3) \times10^{-4}\,\, \mathrm{m}^{-2} \mathrm{sr}^{-1}  \mathrm{s}^{-1}\, \mathrm{GV}^{-1}, \\ 
C_\mathrm{Si}   & =(6.0\pm0.3) \times10^{-4}\,\, \mathrm{m}^{-2} \mathrm{sr}^{-1}  \mathrm{s}^{-1}\, \mathrm{GV}^{-1}. 
\end{align*}
$$

The fit result for Ne, Mg, and Si fluxes together with the 68% C.L. band are also shown in Figure 6.
 
As seen the rigidity dependences of  Ne, Mg, and Si  and He, C, and O are distinctly different.

The previous AMS results on primary cosmic rays He, C, and O show, unexpectedly,  that they have  identical rigidity dependence above 60 GV and that they deviate from a single power law above 200 GV, whereas the secondary cosmic rays Li, Be, and B also  have identical rigidity dependence above 30 GV and deviate from a single power law above 200 GV. The rigidity dependence of primary cosmic rays He, C, and O is distinctly different from secondary cosmic rays Li, Be, and B. These results indicate there are two kinds of cosmic ray rigidity dependences. These observations have generated new developments in cosmic ray models [M.J. Boschini et al., Astrophys. J. 840, 115 (2017); M.J. Boschini et al., Astrophys. J. 858, 61 (2018); C. Evoli, R. Aloisio, and P. Blasi, Phys. Rev. D 99, 103023 (2019); M.J. Boschini et al., Astrophys. J. 889, 167 (2020); N. Weinrich, Y. Génolini, M. Boudaud, L. Derome, and D. Maurin, submitted to Astron. Astrophys. (2020)]. The  theoretical models have their limitations, as none of them predicted the observed spectral behaviour of the  cosmic rays.  The  results on heavier primary cosmic rays Ne, Mg, and Si show that primary cosmic rays have at least two distinct classes of rigidity dependence. These unexpected results together with ongoing measurements of heavier elements in cosmic rays will enable us to determine how many classes of rigidity dependence exist in  both primary  and secondary cosmic rays and provide important information for the development of the theoretical models.