1. Physics

Towards Understanding the Origin of Cosmic-Ray Electrons

We present the precision measurement of the electron flux with a particular emphasis on the behavior at high energies. The measurement is based on 28.1 million electron events collected by AMS from May 19, 2011 to November 12, 2017. This corresponds to a factor of three increase in statistics and factor of two increase in the energy range compared to our results published in 2014 [PRL 113, 121102 (2014)]. The latest precision results on cosmic-ray electrons up to 1.4 TeV reveal new and unexpected features. Our latest data on cosmic-ray electrons and positrons are crucial for providing insights into origins of high energy cosmic-ray electrons and positrons.

We found that in the entire energy range the electron and positron spectra have distinctly different magnitudes and energy dependences. The electron flux exhibits a significant excess starting from $ 42.1_{-5.2}^{+5.4} $ GeV compared to the lower energy trends, but the nature of this excess is different from the positron flux excess above $25.2 \pm 1.8$ GeV. Contrary to the positron flux, which has an exponential energy cutoff of $810_{-180}^{+310} $ GeV, at the 5σ level the electron flux not have an energy cutoff below 1.9 TeV. In the entire energy range the electron flux is well described by the sum of two power law components. The different behavior of the cosmic-ray electrons and positrons measured by AMS clear evidence that most high energy electrons originate from different sources than high energy positrons.

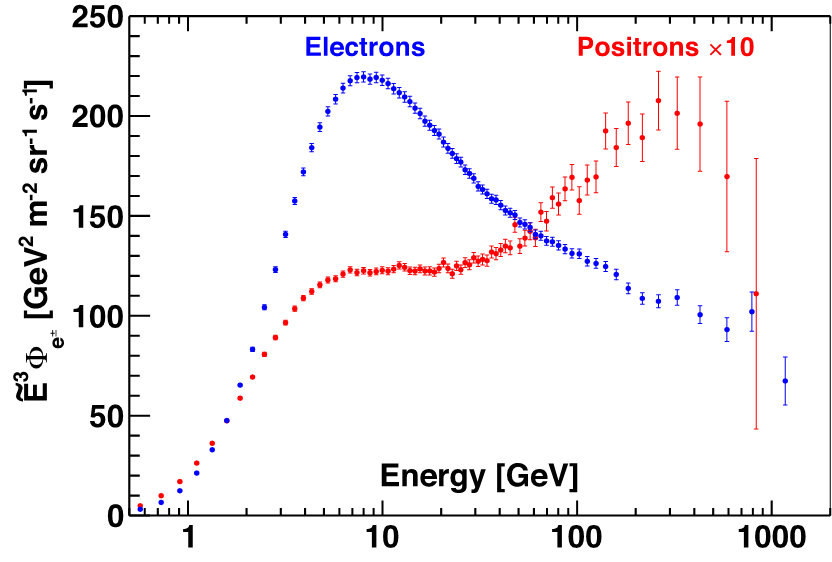
Figure 1 shows the latest AMS results on the precision measurements of the electron spectrum and the positron spectrum from the most recent AMS data. These measurements are based on 28.1 million electron and 1.9 million positron events. 

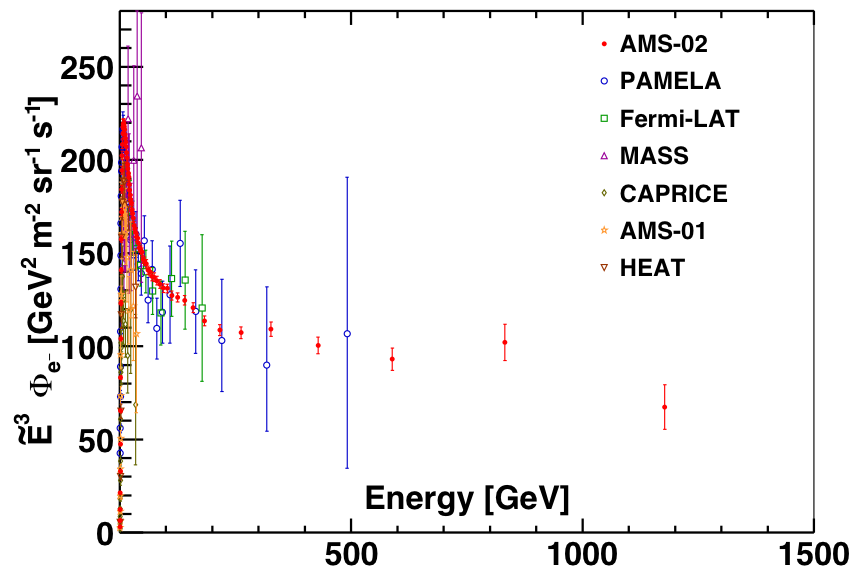
Figure 2 shows the latest AMS results on the precision measurements of the electron spectrum. The other most recent measurements are shown for comparison.

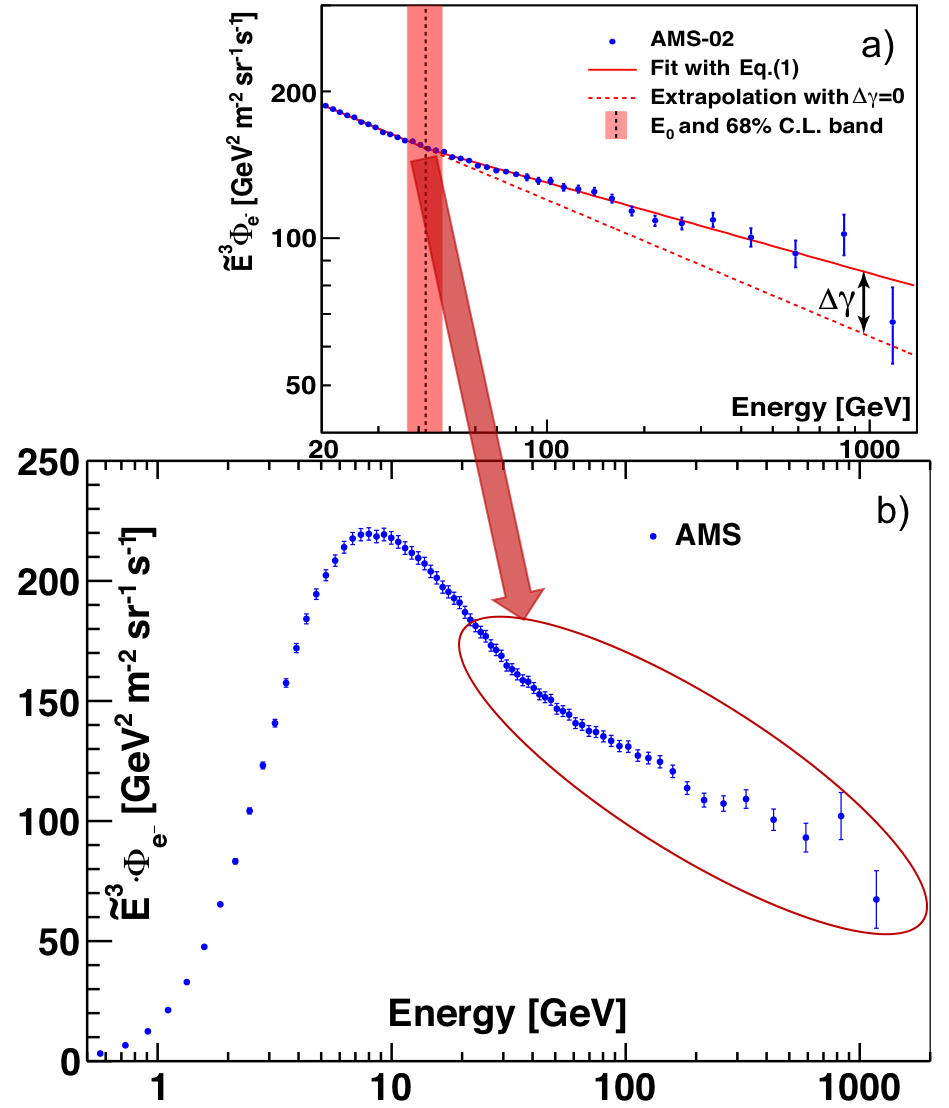
Similar to the analysis of the positron flux, we examine the changing behavior of the electron spectrum using the same power law approximation

$$ \label{eq:1} \Phi_{e^{-}}(E)= \begin{cases} C(E/20.04\mbox{ GeV})^{\gamma}, & E \leq E_{0}; \\ C(E/20.04\mbox{ GeV})^{\gamma}(E/E_{0})^{\Delta\gamma}, & E > E_{0}. \end{cases} \tag{1} $$

A fit to data is performed in the energy range [20.04−1400] GeV. The results are presented in Figure 3. The fit yields $E_{0} = 42.1_{-5.2}^{+5.4}$ GeV for the energy where the spectrum behavior changes. The significance of this change is established at 7σ.

electron and positron spectra
Figure 1. The AMS electron (blue data points) and positron (red data points, multiplied by 10) spectra ($\tilde{E}^{3}\Phi_{e^{\pm}}$). For display purposes the electron data point at ∼830 GeV is slightly shifted horizontally to avoid overlap with the positron point. As seen, the electron spectrum has distinctly different magnitude and energy dependence compared to that of positrons.
electron flux
Figure 2. The AMS cosmic-ray electron flux. For comparison other recent measurements from PAMELA, Fermi-LAT, MASS, CAPRICE, AMS-01, and HEAT are also shown.
fit to electron flux
Figure 3. Fit to the electron flux in the energy range [20.04−1400] GeV. The blue data points are the measured electron spectrum. (a) The fitted power law approximation, Eq. (\ref{eq:1}), is represented by the red line. The vertical dashed line and band correspond to the value and the error of the energy $E_{0}$ where the change of the spectrum occurs. The dashed red line is the extrapolation of the power law below $E_{0}$ into the higher energy region. ∆γ is the magnitude of the spectral index change (7σ effect). The lower graph (b) is for illustration of this changing behavior.

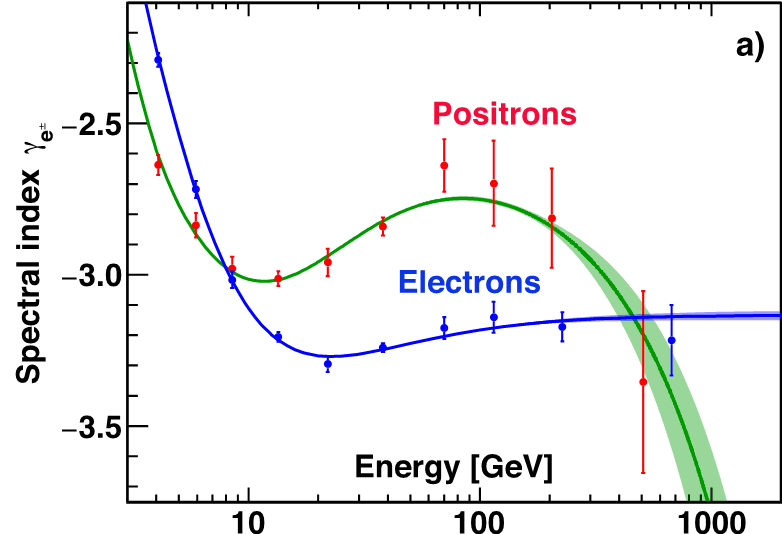
To examine the energy dependence of the electron flux in a model independent way, the flux spectral index $\gamma$ is calculated from $\gamma = d[\log(\Phi)]/d[\log(E)]$ over non-overlapping energy intervals which are chosen to have sufficient sensitivity to the spectral index. The energy interval boundaries are 3.36, 5.00, 7.10, 10.32, 17.98, 27.25, 55.58, 90.19, 148.81, 370 and 1400 GeV. The results are presented in Figure 4 together with the positron results. As seen, both the electron and positron indices decrease (soften) rapidly with energy below ∼10 GeV, and then they both start increasing (harden) at >20GeV. In particular, the electron spectral index increases from $\gamma = −3.295\pm0.026$ in the energy range [17.98 − 27.25] GeV to an average $\gamma = −3.180\pm0.008$ in the range [55.58 − 1400] GeV, where it is nearly energy independent.

As seen in Figure 4, the behavior of the electron and positron spectral indices is distinctly different.

spectral indices of electron flux and of positron flux
Figure 4.  The spectral indices of the electron flux $\gamma_{e^{-}}$ and of the positron flux $\gamma_{e^{+}}$ as a function of energy. The models (Eq. (2) in Origin of Positrons and Eq. (\ref{eq:4})) that fit positron and electron data are represented by the green line and the blue line, respectively. The corresponding bands are at 68% C.L. of the model parameters.

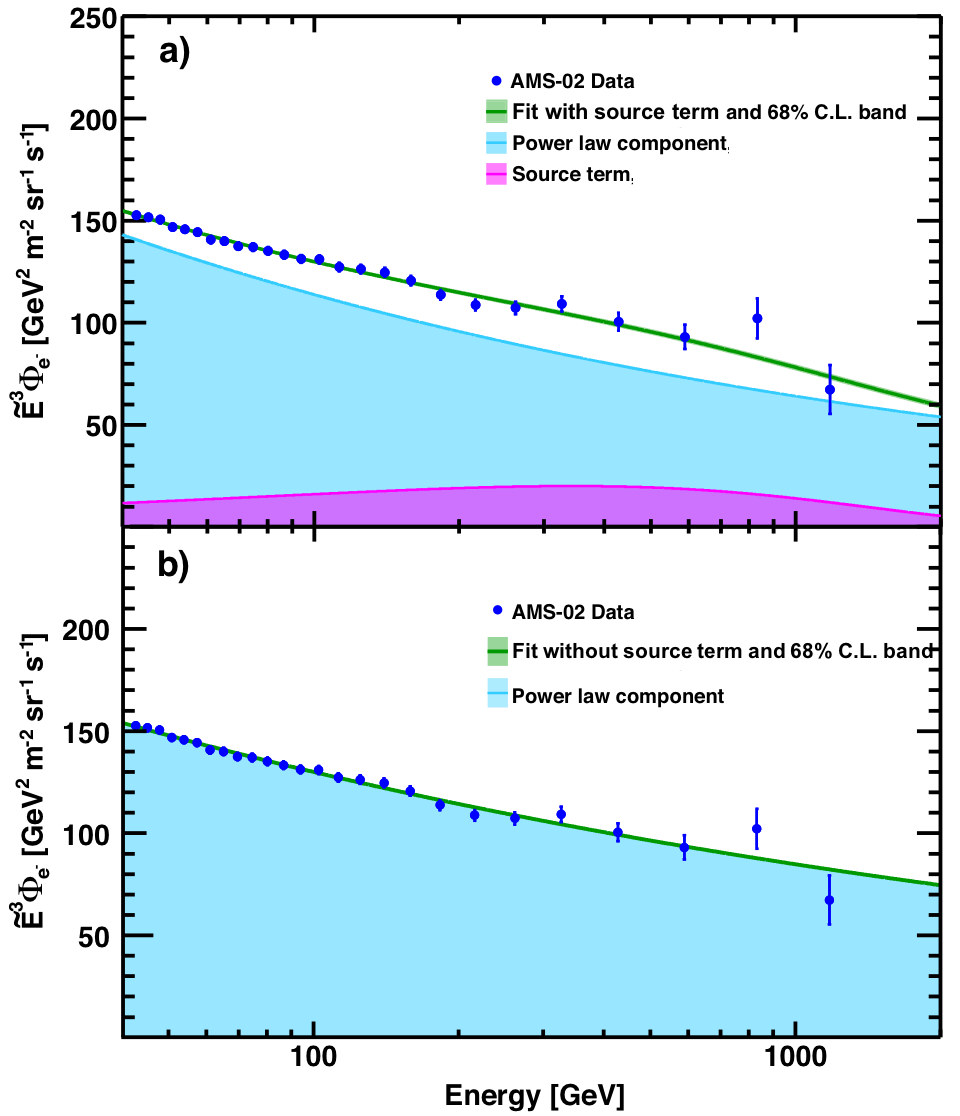
New sources of high energy positrons, such as dark matter, may also produce an equal amount of high energy electrons. We test this hypothesis using the source term from our positron analysis. The electron flux is parametrized as a sum of a power law component and the positron source term with the exponential energy cutoff:

$$ \label{eq:2} \Phi_{e^{-}}(E)= C_{e^{-}}(E/E_{1})^{\gamma_{e^{-}}} + f_{e^{-}}C_{S}^{e^{+}}(E/E_{2})^{\gamma_{S}^{e^{+}}}\exp(-E/E_{S}^{e^{+}}) \tag{2} $$

The power law component is characterized by the normalization factor $C_{e^{-}}$ and the spectral index $\gamma_{e^{-}}$ . The constant $E_1= 41.61$ GeV corresponds to the beginning of the fit range, it does not affect the fitted value of $\gamma_{e^{-}}$ . The values of the source term parameters $C_{S}^{e^{+}}$, $\gamma_{S}^{e^{+}}$, $E_2$ , and $E_{S}^{e^{+}}$ are taken from positron data. A fit to the data with the source term normalization $f_{e^{−}}$ fixed to 1 is performed in the energy range [41.61 − 1400] GeV, where the solar modulation effects are negligible. It yields $C_{e^{-}} = (1.965 \pm 0.010) \times 10^{−3} [ \mathrm{m^{2}\,sr\,s\,GeV}]^{-1}$ and $\gamma_{e^{-}} = −3.248 \pm 0.007$ for the power law component with $\chi^2/\mathrm{d.o.f.} = 15.5/24$. The result of the fit is presented in Figure 5(a).

A similar fit of Eq. (\ref{eq:2}) to data, but with $f_{e^{-}}$ fixed to 0, yields $C_{e^{-}} = (2.124 \pm 0.010) \times 10^{−3} [\mathrm{m^{2}\,sr\,s\,GeV}]^{-1}$ and $\gamma_{e^{-}} = −3.186 \pm 0.006$ with $\chi^2/\mathrm{d.o.f.} = 15.2/24$. The result of this fit is presented in Fig. 5(b). Varying the normalization of the source term $f_{e^{-}}$ as a free fit parameter does not improve the $\chi^2$ and yields $f_{e^{-}} = 0.5_{-0.6}^{+1.2}$ . As seen in Figures 5 (a) and (b) the data are consistent both with the charge symmetric positron source term ($f_{e^{-}} = 1$ in Eq. (\ref{eq:2})) and also with the absence of such a term ($f_{e^{-}} = 0$). Therefore, it is not possible to extract any additional information on the existence and properties of the source term with the electron flux.

fit of a power law
Figure 5. (a) The fit of a power law plus the positron source term (Eq. (\ref{eq:2}), $f_{e^{-}}=1$) to the electron flux data in the energy range [41.61 − 1400] GeV with the 68% C.L. (green band). The source term contribution, identical to that of positrons, is represented by the magenta area and the power law component by the blue area. (b) The fit of a power law (Eq. (\ref{eq:2}), $f_{e^{-}}=0$) to the electron flux data in the energy range [41.61 − 1400] GeV with the 68% C.L. (green band). The power law component is represented by the blue area.

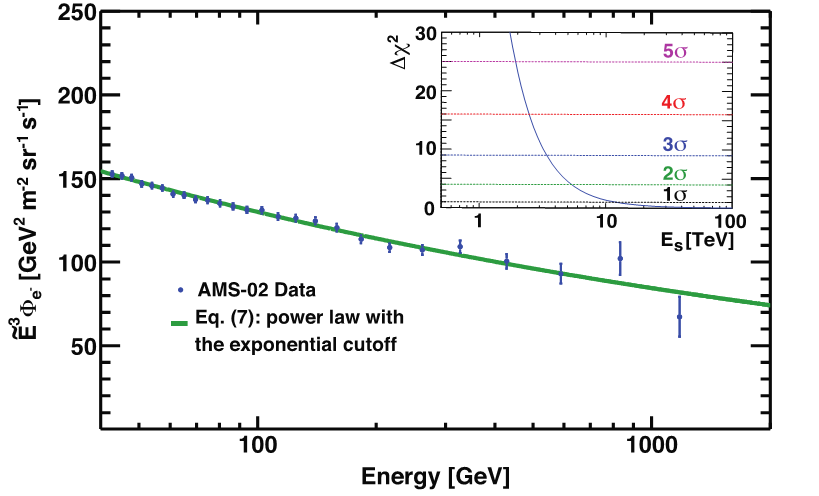
To investigate the existence of a finite energy cutoff as seen in the positron flux, the electron flux is fitted with

$$ \label{eq:3} \Phi_{e^{-}}(E)= C_{S}(E/41.61\mbox{ GeV})^{\gamma_{S}}\exp(-E/E_{S}) \tag{3} $$

A fit to data in the energy range [41.61, 1400] GeV yields the inverse cutoff energy $1/E_{s} = 0.00_{-0.00}^{+0.08}$ TeV−1 with $\chi^2/\mathrm{d.o.f.} = 15.2/23$. A study of the cutoff significance shows that $E_{s} < 1.9$ TeV is excluded at the 5σ level. These results are presented in Figure 6.

fit to the electron flux data
Figure 6.  The fit to the electron flux data in the energy range [41.61−1400] GeV. The insert shows the study of the significance of the $1/E_{s}$ measurement by varying all three fit parameters in Eq. (\ref{eq:3}) to find the minimal $\Delta\chi^{2}$ corresponding to $E_{s}$ values from 1 to 100 TeV. The blue curve shows the dependence of $\Delta\chi^{2}$ on $E_{s}$ and the horizontal dashed lines show different significance levels from 1 to 5σ. As seen, Es values below 1.9 TeV are excluded at the 5σ level.

In addition to a small contribution of secondary electrons produced in the collisions of ordinary cosmic rays with the interstellar gas, there are several astrophysical sources of primary cosmic-ray electrons. It is assumed that there are only a few astrophysical sources of high energy electrons in the vicinity of the solar system each making a power law-like contribution to the electron flux. In addition, there are several physics effects which may introduce some spectral features in the original fluxes. Therefore, it is important to know the minimal number of distinct power law functions needed to accurately describe the AMS electron flux.

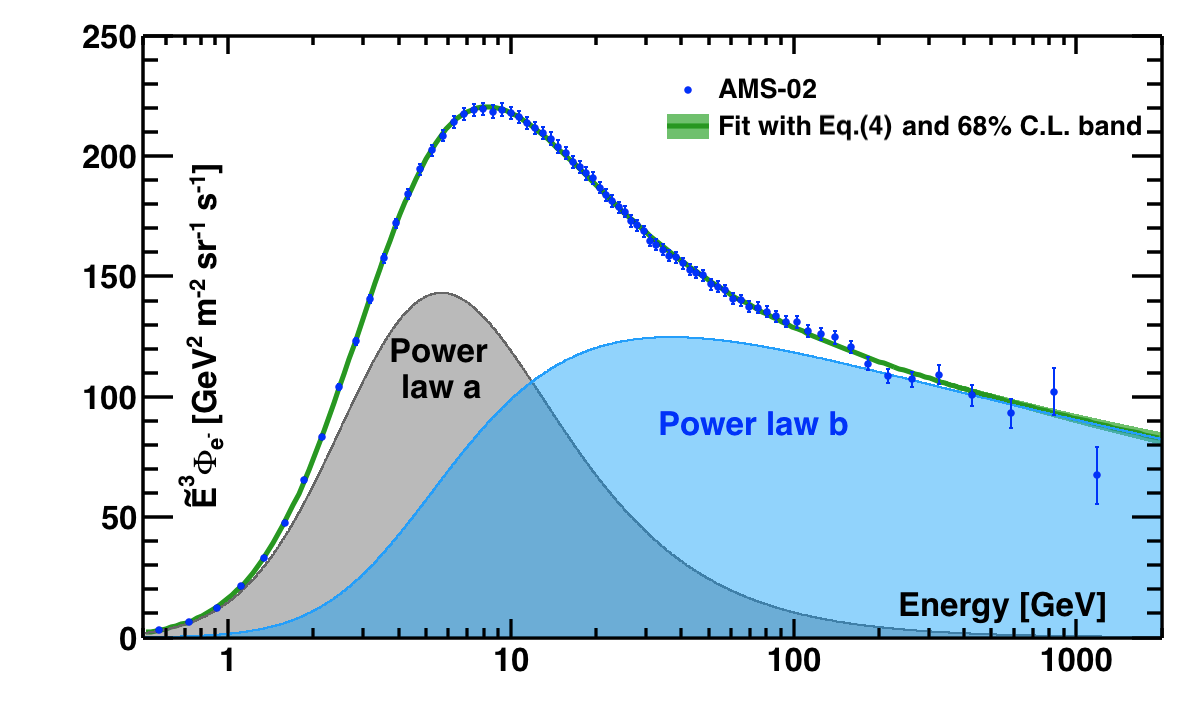
We found that in the entire energy range [0.5 − 1400] GeV the electron flux is well described by the sum of two power law components:

$$ \label{eq:4} \Phi_{e^{-}}(E)= \dfrac{E^{2}}{\hat{E}^{2}}[1+(\hat{E}/E_{t})^{\Delta\gamma_{t}}]^{-1}[C_{a}(\hat{E}/E_{a})^{\gamma_{a}}+C_{b}(\hat{E}/E_{b})^{\gamma_{b}}]  \tag{4} $$

The two components, $a$ and $b$, correspond to two power law functions. To account for solar modulation effects, the force-field approximation is used, with the energy of particles in the interstellar space $\hat{E}=E+\varphi_{e^{-}}$ and the effective modulation potential $\varphi_{e^{-}}$. The additional transition term, $[1+(\hat{E}/E_{t})^{\Delta\gamma_{t}}]^{-1}$, has vanishing impact on the flux behavior at energies above $E_{t}$ (e.g. < 0.7% above 40 GeV). A fit to the data in the energy range [0.5−1400] GeV is presented in Figure 7. We conclude that in the energy range [0.5 − 1400] GeV the sum of two power law functions provides an excellent description of the data with $\chi^{2}/\mathrm{d.o.f.} = 36.5/68$.

two power law fit
Figure 7. The two-power law fit (Eq. (\ref{eq:4})) to the electron flux data in the energy range [0.5 − 1400] GeV with the 68% C.L. (green band). The two power law components $a$ and $b$ are represented by the grey and blue areas, respectively.

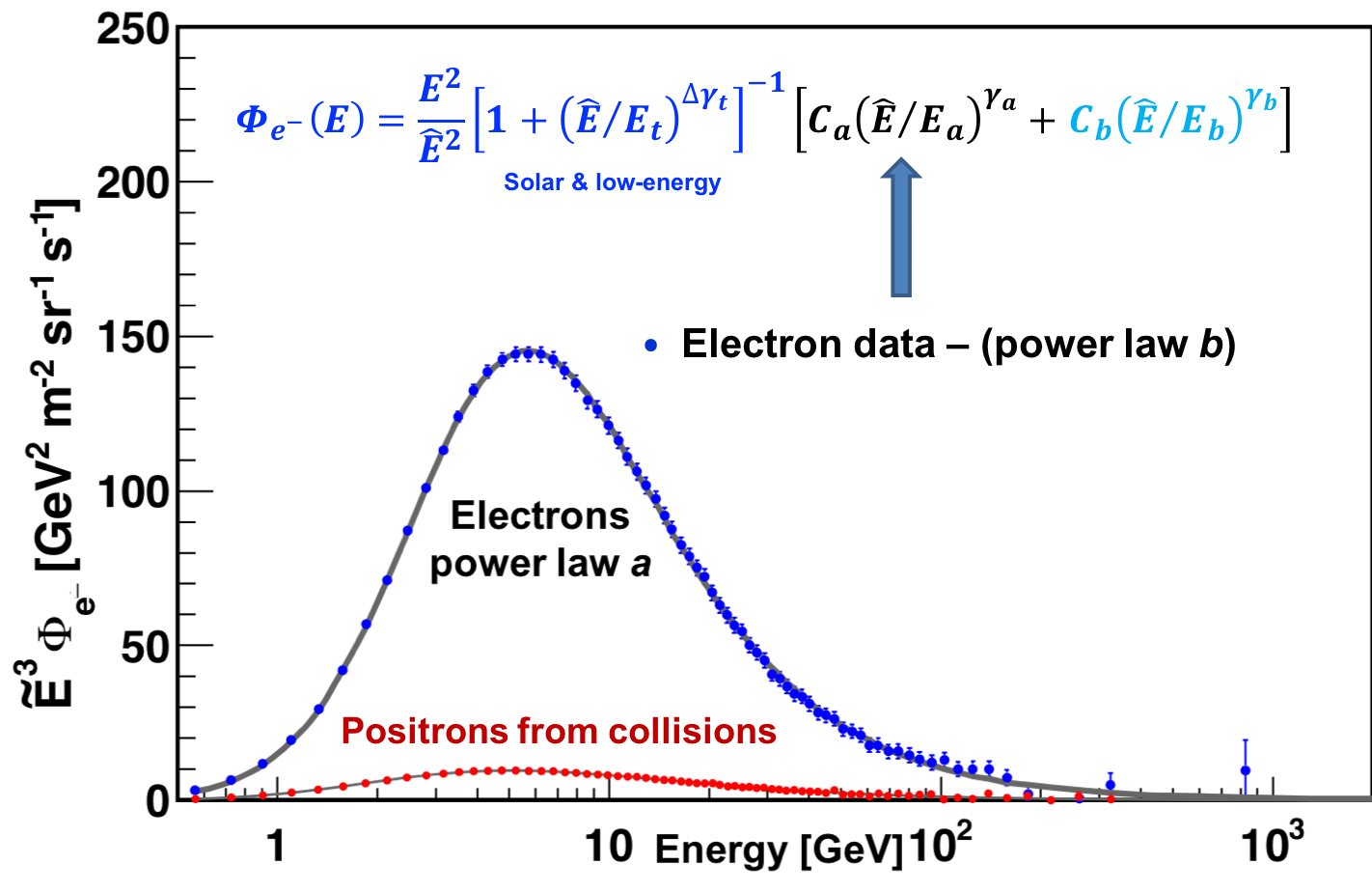
An analysis of the individual components in the electron flux, namely the power law $a$ and $b$ terms, is presented in Figures 8 and 9 together with the corresponding positron data. As seen in Figure 8, at low energies positrons come from cosmic ray collisions, electrons do not. As seen in Figure 9, the positron source term has a cutoff, whereas electrons have neither the source term nor the cutoff.

analysis of the low energy electron power law a data
Figure 8. Analysis of the low energy electron power law $a$ data (i.e. the electron data minus the power law $b$ contribution). For comparison, the positron diffuse term data are also shown.
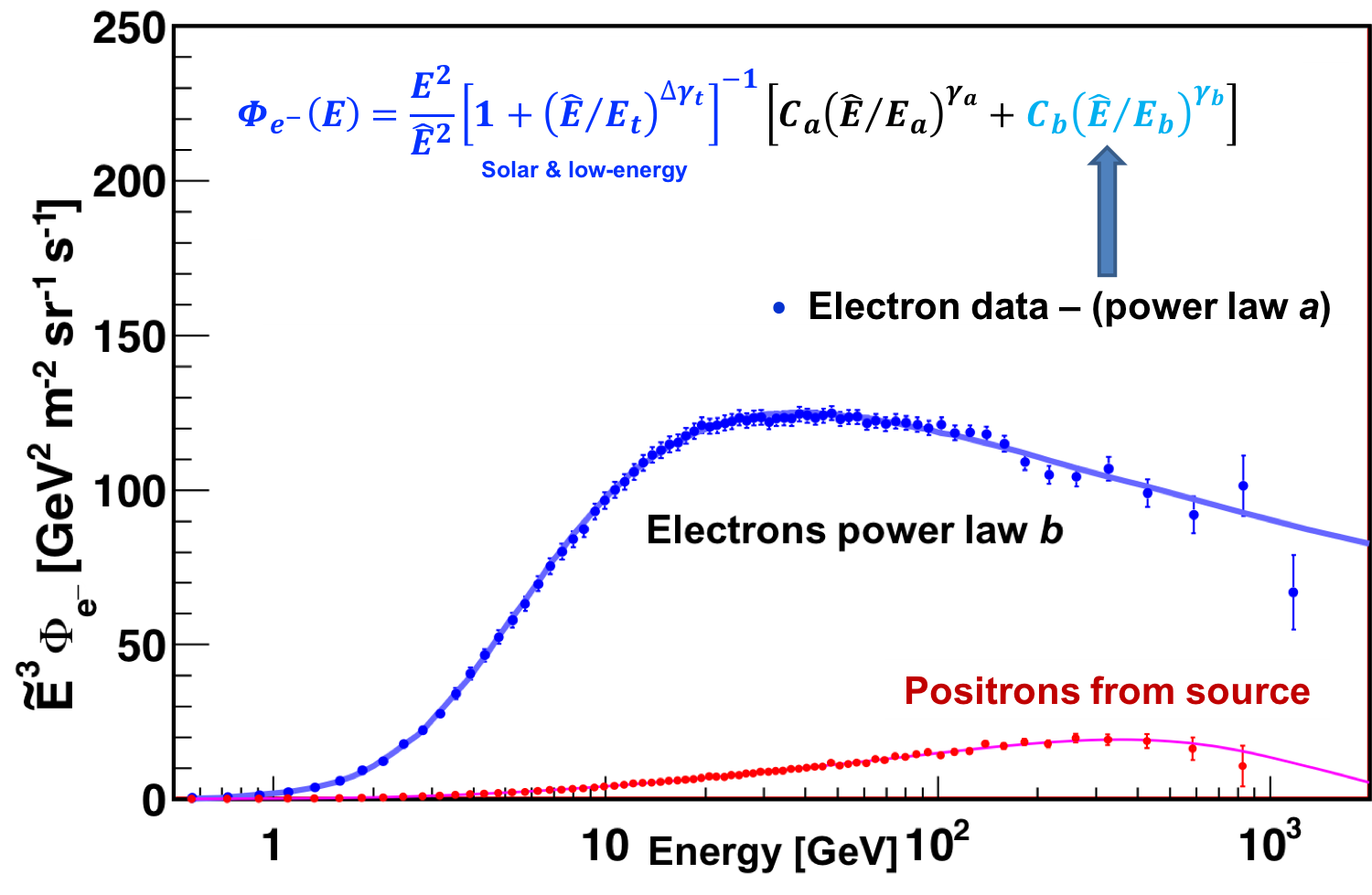
analysis of the electron power law b data
Figure 9. Analysis of the electron power law $b$ data (i.e. the electron data minus the power law $a$ contribution). For comparison, the positron source term data are also shown.

In the entire energy range the electron and positron spectra have distinctly different magnitudes and energy dependences. The different behavior of the cosmic-ray electrons and positrons measured by AMS is clear evidence that most high energy electrons originate from different sources than high energy positrons.

Publication